Optics and Photonics
The past two decades have seen a revolution in the science of light. Photonic (light-manipulating) structures can now be engineered with size comparable to the optical wavelength, allowing us to exploit the wave nature of light to achieve a variety of novel effects. Devices such as photonic crystals, on-chip optical circuits, and microcavity lasers have important technological roles in communications, sensing, and computing. They are also fruitful platforms for basic scientific research.
Topological Photonics
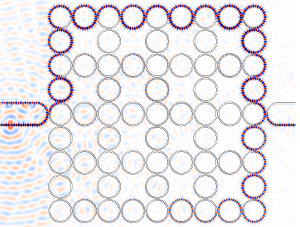 A photonic topological insulator consisting of a lattice of
coupled ring resonators. Light is injected on the left (red
and blue areas showing the positive/negative values of the
electric field), and flows around the edge of the lattice
similar to “topologically-protected” electron edge states in
topological insulator materials.
A photonic topological insulator consisting of a lattice of
coupled ring resonators. Light is injected on the left (red
and blue areas showing the positive/negative values of the
electric field), and flows around the edge of the lattice
similar to “topologically-protected” electron edge states in
topological insulator materials.
Researchers in photonics have long been inspired by a conceptual analogy between electromagnetic waves in patterned dielectric media and quantum mechanical electron waves in solids. In the late 1980s, Eli Yablonovitch and Sajeev John conceived of the photonic crystal as a photonic analog of a conventional electronic insulator. Photonic crystals are now a staple of nanophotonics, with applications ranging from low-loss optical resonators to slow-light wave-guides.
In recent years, researchers have begun to study photonic analogs of insulating materials known as topological insulators, which are mathematically distinct from conventional insulators. A topological insulator possesses a bandgap, but its bands are topologically distinct from the bands of a conventional insulator; it is impossible to smoothly deform one into the other, in the same way that a torus cannot be deformed into a sphere without tearing its surface. As a result, the surface of a topological insulator is populated by “topological edge states” that possess highly unusual properties, such as the ability to travel around sharp corners without backscattering.
Some contributions we have made to this exciting field include:
- A theoretical analysis showing how a periodic lattice of coupled ring resonators can function as a photonic topological insulator with tunable topological phase transitions (Physical Review Letters 2013, Physical Review B 2014).
- The design and implementation of an electromagnetic “topological pump”, an experiment to directly probe the topological features of a bandstructure (Physical Review X 2015).
- Predictions of a range of novel phenomena at the intersection of nonlinear optics and topological photonics, such as solitons that can bypass obstacles (Physical Review Letters 2016) and robust optical valves (New Journal of Physics 2017).
- In collaboration with Mikael C. Rechtsman at PSU, the use of an optical waveguide array to achieve a “Type-II Weyl point”, a topological phenomenon special to three-dimensional media (Physical Review Letters 2016, Nature Physics 2017).
- In collaboration with Wang Qijie at NTU EEE and Zhang Baile at NTU SPMS, the development of the first electrically pumped topological laser, based on terahertz waves circulating around loops with sharp corners (Nature 2020).
Topological Acoustics and Electronics
Apart from photonics, topological edge states can occur in other types of systems that host classical (non quantum mechanical) waves, including sound waves and electrical waves. We have made numerous contributions in these areas, in collaboration with Zhang Baile, including:
- The first theoretical proposal for topological acoutics (Physical Review Letters 2015).
- Using acoustic resonators for pioneering realizations of several novel topological phenomena including “high-order topological insulators” (Nature Materials 2019) and “topological triple points” (Nature Physics 2019).
- Using a nonlinear electric circuit to demonstrate how topological boundary states can be used to enhance harmonic generation (i.e., the production of a higher-frequency wave from a lower-frequency excitation) (Nature Communications 2019).
- Using a specially-interconnected electric circuit to realize a four-dimensional topological insulator, something originally believed to be a purely theoretical construct (Nature Communications 2020).
Non-Hermitian Photonics
Photonic devices containing optical amplification (gain) and/or absorption (loss) do not conserve the electromagnetic energy flowing through them. These so-called “non-Hermitian” systems have long been treated as imperfect variants of “Hermitian” (energy-conserving) systems. Recently, however, researchers have realized that non-Hermitian systems can possess distinct and noteworthy features.
For instance, when gain and loss are simultaneously present in equal and opposite amounts in two halves of a photonic structure, it is said to be PT (parity-time) symmetric. The exotic properties of PT symmetric photonic structures have been studied in great detail by many research groups. Several years ago, we showed theoretically that by tuning the frequency and/or the gain and loss in a PT symmetric structure, one can induce a spontaneous symmetry breaking transition between PT symmetric scattering eigenmodes (which conserve energy) and PT broken pairs of eigenmodes (one damping and one amplifying) (Physical Review Letters 2011). In the most extreme case, a PT symmetric structure can simultaneously function as a coherent perfect absorber and a laser!
We have also worked on bringing the ideas of band topology into non-Hermitian photonics. Our contributions in this area include:
- The theoretical analysis of a novel class of topological edge states that occur only in non-Hermitian lattices (Physical Review Letters 2017).
- The experimental implementation of a non-Hermitian topological pump (Physical Review B 2017), showing how non-Hermiticity alters the standard experimental signatures of a topologically nontrivial bandstructure.
- In collaboration with Mikael C. Rechtsman at PSU, the experimental realization of an “exceptional ring”, a topological feature uniquely associated with non-Hermitian systems (Nature Photonics 2019).
Coherent Perfect Absorbers
 In this simulation, a small disc (much smaller than the
optical wavelength) made of optically absorbing material is
surrounded by larger discs made of non-absorbing dielectric.
When a specially-designed waveform is directed at the
structure, it is perfectly absorbed.
In this simulation, a small disc (much smaller than the
optical wavelength) made of optically absorbing material is
surrounded by larger discs made of non-absorbing dielectric.
When a specially-designed waveform is directed at the
structure, it is perfectly absorbed.
Coherent perfect absorption is a phenomenon in which a photonic structure absorbs all of a specially-designed incoming optical wave. The absorption is “perfect”: all of the input light energy is delivered into the material of the photonic structure. (The energy subsequently flows out to an external reservoir, e.g. in the form of heat or electric current.)
Theoretically, coherent perfect absorption is tied to the time-reversal symmetry of electromagnetism, which states that if one process is allowed, then so is a time-reversed process which reverses all currents, spins, and magnetic fields. Several years ago, we published a theoretical paper pointing out that since the field emitted by a laser is a purely-outgoing electromagnetic wave, the time-reversal symmetry operation maps a laser into an “anti-laser” structure, which exhibits perfect absorption of a certain incoming wave — the time reverse of the laser field (Physical Review Letters 2010).
Coherent perfect absorption is a generalization of the concept of “critical coupling”. We demonstrated the principle experimentally (Science 2011). We have extended the concept in various ways. For instance, we have shown theoretically that in weakly-absorbing “random media”, such as foam, paint, or tissue, a specially-designed input wave-front can achieve extremely strong absorption even if the medium is ordinarily “white” (Physical Review Letters 2010).
We have also written a review article on the topic (Nature Reviews Materials 2017).

